Knot Theory in 2025 Math Exam

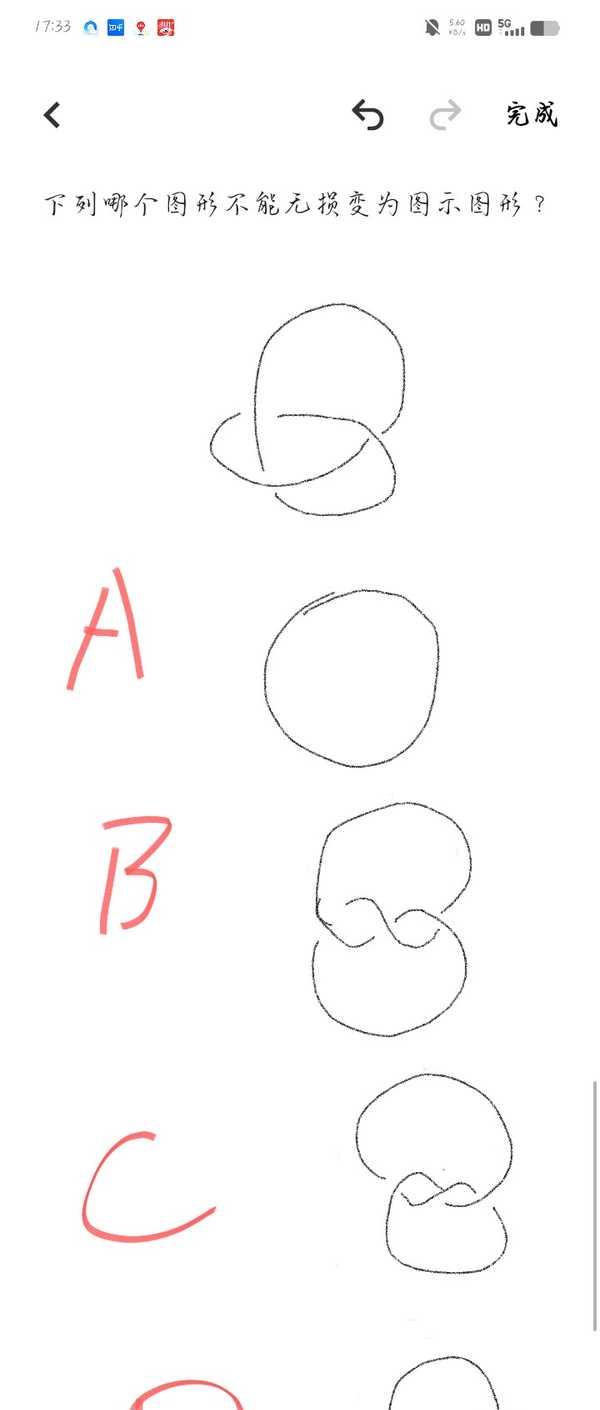
The appearance of knot theory in China’s 2025 Eight-Province Joint College Entrance Examination has sparked intense discussion among educators and students. This unprecedented inclusion of topology-related content in a high school examination represents a significant shift in mathematical assessment approaches.

The question presents students with different knot configurations and asks them to determine which transformations are possible without breaking the knots. While seemingly straightforward, this problem actually touches upon fundamental concepts in knot theory - a sophisticated branch of topology typically encountered at the university level.

The mathematical depth of this question is remarkable. It explores the concept of ambient isotopy, which determines whether two knots can be continuously deformed into each other without breaking. The distinction between left-handed and right-handed trefoil knots, which appears in one of the options, is particularly notable as it requires understanding of topological invariants like the Jones polynomial to prove rigorously.

Many students and teachers have expressed concern about the appropriateness of including such advanced mathematical concepts in a high school examination. The question essentially tests spatial visualization abilities and intuitive understanding of three-dimensional transformations, skills that are valuable but rarely explicitly developed in traditional high school mathematics curricula.

This examination question has broader implications for mathematics education in China. It suggests a potential shift toward incorporating more modern mathematical concepts and emphasizing conceptual understanding over procedural fluency. Some educators argue this approach helps identify students with exceptional mathematical insight, while others worry it may disadvantage students who excel in traditional computational mathematics.

Practical approaches to solving this problem have emerged from the student community. Some suggested using physical objects like string or headphone cables to experiment with the knot transformations. This hands-on approach demonstrates how abstract mathematical concepts can be explored through concrete manipulation, though proving the results formally would require advanced mathematical tools beyond high school level.

The controversy surrounding this question reflects an ongoing debate in mathematical education about the balance between traditional computational skills and conceptual understanding. It raises important questions about the role of advanced mathematical topics in secondary education and the evolving nature of mathematical assessment in China’s educational system.

For prospective students, this development suggests the importance of developing strong spatial reasoning skills and the ability to engage with unfamiliar mathematical concepts. It also highlights how modern mathematics education increasingly values creative problem-solving approaches alongside traditional analytical skills.

The inclusion of knot theory in this high-stakes examination may signal a broader trend toward incorporating more diverse and sophisticated mathematical concepts in secondary education. This could lead to significant changes in how mathematics is taught and assessed in Chinese high schools in the coming years.